Parsing in SQL
SQL is a high abstraction-level language used exclusively as an interface to Relational Databases. Initially it lacked recursion, and, therefore, had a limited expression power, but eventually this construct has been added to the language. Here we'll explore how convenient SQL is for general-purpose programming.
SQL programming is very unusual from procedural perspective: there is no explicit flow control, in general, and no loops, in particular, no variables either to apply operations to, or to store intermediate results into. SQL heavily leverages predicates instead.
Our goal is writing a simple predicate expression parser in SQL. Given an expression like this,
(((a=1 or b=1) and (y=3 or z=1)) and c=1 and x=5 or z=3 and y>7)
the parser should output a tree like this:
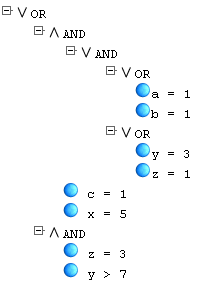
Recursive descent parser is the easy way to approach the task. Unfortunately, Oracle didn’t implement recursion yet, and as I work for Oracle, it clearly is the database of my choice. In cases where a programmer can’t use recursion, (s)he resorts to iteration.
We approach the task by building the set of all subclauses, and then selecting only “well formed” expressions. It’s clearly more work than in procedural programming, but that’s typical SQL attitude: write a query first and let optimizer worry about efficiency.
In order to generate all the subclauses we need a table of integers. Before Oracle 9i we had to take a real table, and add a pseudo column like this:
select rownum from all_objects
where “all_objects” is a “big enough” table. In Oracle 9i we use table function instead:
CREATE TYPE IntSet AS TABLE OF Integer;
/
CREATE or replace FUNCTION UNSAFE
RETURN IntSet PIPELINED IS
i INTEGER;
BEGIN
i := 0;
loop
PIPE ROW(i);
i:=i+1;
end loop;
select rownum from TABLE(UNSAFE) where rownum < 1000
The UNSAFE function is rows producer and the above query is rows consumer. The producer generates a set of rows that fills in the buffer, and then pauses until all those rows are consumed by the query. The process repeats until either producer doesn’t have any rows or a consumer signals that it doesn’t need any more rows.
The first possibility can be implemented as a function with a parameter that will determine when to exit the loop, but in our case it’s a consumer who signals producer to stop. It could also be viewed as if the “rowrun < 1000” predicate were pushed down into the UNSAFE function. Be wary, however, because this predicate pushing works for rownum only. A cautious reader might want to convert the stop predicate into a parameter to the function, but in author’s opinion that solution would have less “declarative spirit.”
The UNSAFE function is the procedural code that formally disqualifies the solution as being pure SQL. In my opinion, however, writing generic PL/SQL functions like integer sequence generator is very different from application-specific PL/SQL code. Essentially, we extend RDBMS engine functionality, which is similar to what built-in SQL functions do.
Now, with iteration abilities we have all the ingredients for writing the parser. Like traditional software practice we start by writing a unit test first:
WITH src as(
select
'(((a=1 or b=1) and (y=3 or z=1)) and c=1 and x=5 or z=3 and y>7)'
exprfrom dual
), …
We refactored the “src” subquery into a separate view, because it would be used in multiple places. Oracle isn’t automatically refactoring the clauses that aren’t explicitly declared so.
Next, we find all delimiter positions:
), idxs as (
select i
from (select rownum i from TABLE(UNSAFE) where rownum < 4000) a, src
where i<=LENGTH(EXPR) and (substr(EXPR,i,1)='('
or substr(EXPR,i,1)=' ' or substr(EXPR,i,1)=')' )
The “rownum<4000” predicate effectively limits parsing strings to 4000 characters only. In an ideal world this predicate wouldn’t be there. The subquery would produce rows indefinitely until some outer condition signaled that the task is completed so that producer could stop then.
Among those delimiters, we are specifically interested in positions of all left brackets:
), lbri as(
select i from idxs, src
where substr(EXPR,i,1)='('
The right bracket positions view - rbri, and whitespaces – wtsp are defined similarly. All these three views can be defined directly, without introduction of idxs view, of course. However, it is much more efficient to push in predicates early, and deal with idxs view which has much lower cardinality than select rownum i from TABLE(UNSAFE) where rownum < 4000.
Now that we have indexed and classified all the delimiter positions, we’ll build a list of all the clauses, which begins and ends at the delimiter positions, and, then, filter out the unrelevant clauses. We extract the segment’s start and end points, first:
), begi as (
select i+1 x from wtsp
union all
select i x from lbri
union all
select i+1 x from lbri
), endi as ( -- [x,y)
select i y from wtsp
union all
select i+1 y from rbri
union all
select i y from rbri
Note, that in case of brackets we consider multiple combinations of clauses - with and without brackets.
Unlike starting point, which is included into a segment, the ending point is defined by an index that refers the first character past the segment. Essentially, our segment is what is called semiopen interval in math. Here is the definition:
), ranges as ( -- [x,y)
select x, y from begi a, endi b
where x < y
We are almost half way to the goal. At this point a reader might want to see what clauses are in the “ranges” result set. Indeed, any program development, including nontrivial SQL query writing, assumes some debugging. In SQL the only debugging facility available is viewing an intermediate result.
Next step is admitting “well formed” expressions only:
), wffs1 as (
select x, y from ranges r
--
-- bracket balance:
where (select count(1) from lbri where i between x and y-1)
= (select count(1) from rbri where i between x and y-1)
--
-- eliminate '...)...(...'
and (select coalesce(min(i),0) from lbri where i between x and y-1)
<= (select coalesce(min(i),0) from rbri where i between x and y-1)
The first predicate verifies bracket balance, while the second one eliminates clauses where right bracket occurs earlier than left bracket.
Some expressions might start with left bracket, end with right bracket and have well formed bracket structure in the middle, like (y=3 or z=1) , for example. We truncate those expressions to y=3 or z=1:
), wffs as (
select x+1 x, y-1 y from wffs1 w
where (x in (select i from lbri)
and y-1 in (select i from rbri)
and not exists (select i from rbri where i between x+1 and y-2
and i < all(select i from lbri where lbri.i
between x+1 and y-2))
)
union all
select x, y from wffs1 w
where not (x in (select i from lbri)
and y-1 in (select i from rbri)
and not exists (select i from rbri where i between x+1 and y-2
and i < all(select i from lbri where lbri.i
between x+1 and y-2))
)
Now that the clauses don’t have parenthesis problems we are ready for parsing Boolean connectives. First, we are indexing all “or” tokens
), andi as (
select x i
from wffs a, src s
where lower(substr(EXPR, x, 3))='or'
and, similarly, all “and” tokens. Then, we identify all formulas that contain “or” connective
), or_wffs as (
select x, y, i from ori a, wffs w where x <= i and i <= y
and (select count(1) from lbri l where l.i between x and a.i-1)
= (select count(1) from rbri r where r.i between x and a.i-1)
and also “and” connective
), and_wffs as (
select x, y, i from andi a, wffs w where x <= i and i <= y
and (select count(1) from lbri l where l.i between x and a.i-1)
= (select count(1) from rbri r where r.i between x and a.i-1)
and (x,y) not in (select x,y from or_wffs ww)
The equality predicate with aggregate count clause in both cases limits the scope to outside of the brackets. Connectives that are inside the brackets naturally belong to the children of this expression where they will be considered as well. The other important consideration is nonsymmetrical treatment of the connectives, because “or” has lower precedence than “and.” All other clauses that don’t belong to either “or_wffs” or “and_wffs” category are atomic predicates:
), other_wffs as (
select x, y from wffs w
minus
select x, y from and_wffs w
minus
select x, y from or_wffs w
Given a segment “- or_wffs,” for example, generally, there would be a segment of same type enclosing it. The final step is selecting only maximal segments; essentially, only those are valid predicate formulas:
), max_or_wffs as (
select distinct x, y from or_wffs w
where not exists (select 1 from or_wffs ww
where ww.x<w.x and w.y<=ww.y and w.i=ww.i)
and not exists (select 1 from or_wffs ww
where ww.x<=w.x and w.y<ww.y and w.i=ww.i)
and similarly defined “max_and_wffs” and “max_other_wffs.” These three views allow us to define:
), predicates as (
select 'OR' typ, x, y, substr(EXPR, x, y-x) expr
from max_or_wffs r, src s
union all
select 'AND', x, y, substr(EXPR, x, y-x)
from max_and_wffs r, src s
union all
select '', x, y, substr(EXPR, x, y-x)
from max_other_wffs r, src s
This view contains the following result set:
| TYP | X | Y | EXPR |
| OR | 2 | 64 | ((a=1 or b=1) and (y=3 or z=1)) and c=1 and x=5 or z=3 and y>7 |
| OR | 4 | 14 | a=1 or b=1 |
| OR | 21 | 31 | y=3 or z=1 |
| AND | 2 | 49 | ((a=1 or b=1) and (y=3 or z=1)) and c=1 and x=5 |
| AND | 3 | 32 | (a=1 or b=1) and (y=3 or z=1) |
| AND | 2 | 49 | z=3 and y>7 |
| 61 | 64 | y>7 | |
| 53 | 56 | z=3 | |
| 46 | 49 | x=5 | |
| 38 | 41 | c=1 | |
| 28 | 31 | z=1 | |
| 21 | 24 | y=3 | |
| 11 | 14 | b=1 | |
| 4 | 7 | a=1 |
How would we build a hierarchy tree out of these data? Easy: the [X,Y) segments are essentially Celko’s Nested Sets.
Oracle 9i added two new columns to the PLAN_TABLE: access_predicates and filter_predicates. Our parsing technique allows extending plan queries and displaying predicates as expression subtrees:

--
Vadim Tropashko works for Real World Performance group at Oracle Corp. In prior life he was application programmer and translated “The C++ Programming Language” by B.Stroustrup, 2nd edition into Russian. His current interests include SQL Optimization, Constraint Databases, and Computer Algebra Systems.
Contributors : Vadim Tropashko
Last modified 2005-02-28 04:45 PM

It is wonderful article, which shows the capabilities of Oracle 9i SQL. We would appreciate if you can post the complete code listing for this article. We have a similar requirement in one of our projects.
Thanks and keep up the good work!
Replies to this comment