Graphs, Trees, and Hierarchies
from the new book, Trees and Hierarchies in SQL for Smarties (Morgan-Kaufmann), 2003.
Let’s start with a little mathematical background. Graph theory is a branch of mathematics that deals with abstract structures, known as graphs. These are not the presentation charts that you get out of a spreadsheet package.
Very loosely speaking, a graph is a diagram of “dots” (called nodes or vertices) and “lines” (edges) that model some kind of “flow” or relationship. The edges can be undirected or directed. Graphs are very general models. In circuit diagrams the edges are the wires and the nodes are the components. On a road map the nodes are the towns and the edges are the roads. Flowcharts, organizational charts, and a hundred other common abstract models you see every day are all shown as graphs.
A directed graph allows a “flow” along the edges in one direction only, as shown by the arrowheads, whereas an undirected graph allows the flow to travel in both directions. Exactly what is flowing depends on what you are modeling with the graph.
The convention is that an edge must join two (and only two) nodes. This lets us show an edge as an ordered pair of nodes, such as (Atlanta, Boston) if we are dealing with a map, or (a, b) in a more abstract notation. There is an implication in a directed graph that the direction is shown by the ordering. In an undirected graph we know that (a, b) = (b, a), however.
A node can sit alone or have any number of edges associated with it. A node can also be self-referencing, as in (a, a).
The terminology used in graph theory will vary, depending on which book you had in your finite math class. The following list, in informal language, includes the terms I will use in this book.
Order of a graph: number of nodes in the graph
Degree: the number of edges at a node, without regard to whether the graph is directed or undirected
Indegree: the number of edges coming into a node in a directed graph
Outdegree: the number of edges leaving a node in a directed graph Subgraph: a graph that is a subset of another graph’s edges and nodes
Walk: a subgraph of alternating edges and nodes that are connected to each other in such a way that you can trace around it without lifting your finger
Path: a subgraph that does not cross over itself—there is a starting node with degree one, an ending node with degree one, and all other nodes have degree two.It is a special case of a walk. It is a “connect-the-dots” puzzle.
Cycle: a subgraph that “makes a loop,” so that all nodes have degree two. In a directed graph all the nodes of a cycle have outdegree one and indegree one (Figure 1.1).
Connected graph: a graph in which all pairs of nodes are connected by a path. Informally, the graph is all in one piece.
Forest: a collection of separate trees. Yes, I am defining this term before we finally get to discussing trees.
There are a lot more terms to describe special kinds of graphs, but frankly, we will not use them in this book. We are supposed to be learning SQL programming, not graph theory.
The strength of graphs as problem-solving tools is that the nodes and edges can be given extra attributes that adapt this general model to a particular problem.
Edges can be assigned “weights,” such as expected travel time for the roads on a highway map. Nodes can be assigned “colors” that put them into groups, such as men and women. Look around and you will see how they are used.
Modeling a Graph in a Program
Long before there was SQL, programmers represented graphs in the programming language that they had. People used pointer chains in assembly language or system development languages such as ‘C’ to build very direct representations of graphs with machine language instructions. However, unlike the low level system development languages, the later, higher-level languages, such as Pascal, LISP, and PL/I, did not expose the hardware to the programmer. Pointers in these higher level languages were abstracted to hide references to the actual physical storage and often required that the pointers point to variables or structures of a particular type. (See PL/I’s ADDR() function, pointer datatypes, and based variables as examples of this kind of language construct.)
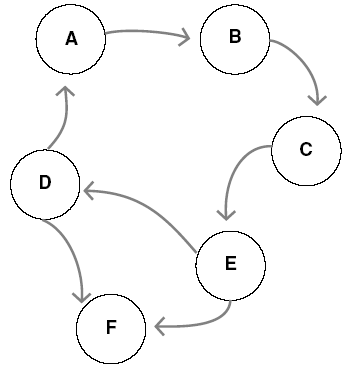
Figure 1.1: Modeling a graph in a program.
Traditional application development languages do not have pointers, but they often have arrays. In particular, FORTRAN only had arrays for a data structure; a good FORTRAN programmer could use them for just about anything. Early versions of FORTRAN did not have character-string data types—everything was either an integer or a floating-point number. This meant the model of a graph had to be created by numbering the nodes and using the node numbers as subscripts to index into the arrays.
Once the array techniques for graphs were developed, they became part of the “programmer’s folklore” and were implemented in other languages. I will use a pseudocode to explain the techniques.
Adjacency Lists for Graphs
The adjacency list model represents the edges of the graph as pairs of nodes, similar to the following computer code:
DECLARE ARRAY GraphList
OF RECORD [edge CHAR(1), in_node INTEGER, out_node INTEGER];
With data:
GraphList
edge in_node out_node
‘a’ 1 2
‘b’ 2 3
‘c’ 4 2
‘d’ 1 4
The algorithms that we used were based on loops that made the connections between two edges, in which the in_node of one row was equal to the out_node of another row.
Adjacency Arrays for Graphs
Many of the computational languages had library functions for matrix operations; therefore it was logical to put the graph into an array where it could be manipulated with these functions.
Given (n) nodes, you could declare an (n) by (n) array with zeros and ones in the cells. A “one” meant that there was an edge between the two nodes represented by the row and column of the cell, and a “zero” meant that there was not.
You can actually represent a two-dimensional array; for example: A[0:5, 0:5], with a table like this:
CREATE TABLE Array_A
(edge CHAR(10) NOT NULL,
i INTEGER NOT NULL UNIQUE
CHECK (i BETWEEN 0 AND 5),
j INTEGER NOT NULL UNIQUE
CHECK (j BETWEEN 0 AND 5),
PRIMARY KEY (i, j));
I have a chapter in SQL For Smarties on how to do basic matrix math with such tables. However, because SQL was not meant to be used this way, the code to implement the old Adjacency Array algorithms is rather baroque. Array was added to SQL-99 as a “collection type” for columns, but it is not widely implemented and has serious limitations — it is a vector, or one-dimensional array, and not a full multidimensional structure.
Finding a Path in General Graphs in SQL
There is a classic problem in graph theory that illustrates how expensive it can be to do general graphs in SQL. What we want is a list of paths from any two nodes in a directed graph in which the edges have a weight. The sum of these weights gives us the cost of each path so that we can pick the cheapest path. The best way is probably to use the Floyd-Warshall or Johnson algorithm in a procedural language and load a table with the results. However, I want to do this in pure SQL as an exercise. Let’s start with a simple graph and represent it as an adjacency list with weights on the edges.
CREATE TABLE Graph
(source CHAR(2) NOT NULL,
destination CHAR(2) NOT NULL,
cost INTEGER NOT NULL,
PRIMARY KEY (source, destination));
I obtained data for this table from the book Introduction to Algorithms by Cormen, Leiserson, and Rivest (Cambridge, Mass., MIT Press, 1990, p. 518; ISBN 0-262-03141-8). This book is very popular in college courses in the United States. I made one decision that will be important later—I added selftraversal edges—the node is both the source and the destination so the cost of those paths is zero.
INSERT INTO Graph
VALUES (‘s’, ‘s’, 0),
(‘s’, ‘u’, 3),
(‘s’, ‘x’, 5),
(‘u’, ‘u’, 0),
(‘u’, ‘v’, 6),
(‘u’, ‘x’, 2),
(‘v’, ‘v’, 0),
(‘v’, ‘y’, 2),
(‘x’, ‘u’, 1),
(‘x’, ‘v’, 4),
(‘x’, ‘x’, 0),
(‘x’, ‘y’, 6),
(‘y’, ‘s’, 3),
(‘y’, ‘v’, 7),
(‘y’, ‘y’, 0);
I am not happy about this approach, because I have to decide the maximum number of edges in a path before I start looking for an answer. However, this will work, and I know that a path will have no more than the total number of nodes in the graph. Let’s create a table to hold the paths:
CREATE TABLE Paths
(step_1 CHAR(2) NOT NULL,
step_2 CHAR(2) NOT NULL,
step_3 CHAR(2) NOT NULL,
step_4 CHAR(2) NOT NULL,
step_5 CHAR(2) NOT NULL,
total_cost INTEGER NOT NULL,
path_length INTEGER NOT NULL,
PRIMARY KEY (step_1, step_2, step_3, step_4, step_5));
The step_1 node is where I begin the path. The other columns are the second step, third step, fourth step, and so forth. The last step column is the end of the journey. The total_cost column is the total cost, based on the sum of the weights of the edges, on this path. The path_length column is harder to explain, but for now let’s just say that it is a count of the nodes visited in the path.
To keep things easier let’s look at all the paths from “s” to “y” in the graph. The INSERT INTO statement for constructing that set looks like this:
INSERT INTO Paths
SELECT
G1.source, it is ‘s’ in this example
G2.source,
G3.source,
G4.source,
G4.destination, it is ‘y’ in this example
(G1.cost + G2.cost + G3.cost + G4.cost),
(CASE WHEN G1.source
NOT IN (G2.source, G3.source, G4.source)
THEN 1 ELSE 0 END
+ CASE WHEN G2.source
NOT IN (G1.source, G3.source, G4.source)
THEN 1 ELSE 0 END
+ CASE WHEN G3.source
NOT IN (G1.source, G2.source, G4.source)
THEN 1 ELSE 0 END
+ CASE WHEN G4.source
NOT IN (G1.source, G2.source, G3.source)
THEN 1 ELSE 0 END)
FROM Graph AS G1, Graph AS G2, Graph AS G3, Graph AS G4
WHERE G1.source = ‘s’ AND G1.destination = G2.source
AND G2.destination = G3.source
AND G3.destination = G4.source
AND G4.destination = ‘y’;
I put in “s” and “y” as the source and destination of the path and made sure that the destination of one step in the path was the source of the next step in the path. This is a combinatorial explosion, but it is easy to read and understand.
The sum of the weights is the cost of the path, which is easy to understand. The path_length calculation is a bit harder. This sum of CASE expressions looks at each node in the path. If it is unique within the row, it is assigned a value of one; if it is not unique within the row, it is assigned a value of zero.
All paths will have five steps in them, because that is the way the table is declared. However, what if a path shorter than five steps exists between the two nodes? That is where the self-traversal rows are used! Consecutive pairs of steps in the same row can be repetitions of the same node. Here is what the rows of the paths table look like after this INSERT INTO statement, ordered by descending path_length, and then by ascending cost:
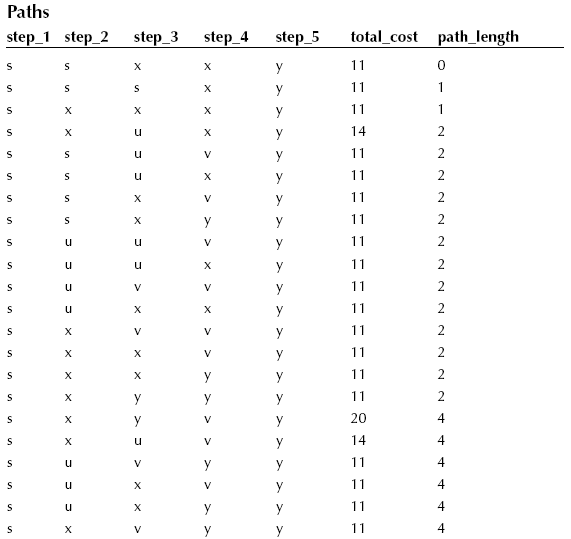
Many of these rows are equivalent to each other. For example, the paths (‘s’, ‘x’, ‘v’, ‘v’, ‘y’, 11, 2) and (‘s’, ‘x’, ‘x’, ‘v’, ‘y’, 11, 2) are both really the same path as (‘s’, ‘x’, ‘v’, ‘y’).
In this example the total_cost column defines the cost of a path, so we can eliminate some of the paths from the table with this statement, if we want the lowest cost.
DELETE FROM Paths
WHERE total_cost
> (SELECT MIN(total_cost)
FROM Paths);
In this example, it got rid of three out of 22 possible paths. Let’s consider another cost factor: the number of paths. People do not like to change airplanes or trains en route to their destination. If they can go from Amsterdam to New York without changing planes, for the same cost, they are happy. This is where that path_length column comes in. It is a quick way to remove the paths that have more edges than they need to get the job done.
DELETE FROM Paths
WHERE path_length
> (SELECT MIN(path_length)FROM Paths);
In this case that last DELETE FROM statement will reduce the table to one row (‘s’, ‘s’, ‘x’, ‘x’, ‘y’, 11, 0), which reduces to (‘s’, ‘x’, ‘y’). This single remaining row is very convenient for my demonstration, but if you look at the table, you will see that there was also a subset of equivalent rows that had higher path_length numbers.
(‘s’, ‘s’, ‘s’, ‘x’, ‘y’, 11, 1)
(‘s’, ‘x’, ‘x’, ‘x’, ‘y’, 11, 1)
(‘s’, ‘x’, ‘x’, ‘y’, ‘y’, 11, 2)
(‘s’, ‘x’, ‘y’, ‘y’, ‘y’, 11, 2)
Your task is to write code to handle equivalent rows. Hint: the duplicate nodes will always be contiguous across the row. There is an important difference between a tree and a hierarchy, which has to do with inheritance and subordination. Trees are a special case of graphs; hierarchies are a special case of trees. Let’s start by defining trees.
Trees
Trees are graphs that have the following properties:
- A tree is a connected graph that has no cycles. A connected graph is one in which there is a path between any two nodes. No node sits by itself, disconnected from the rest of the graph.
- Every node is the root of a subtree. The most trivial case is a subtree of only one node.
- Every two nodes in the tree are connected on one (and only one) path.
- A tree is a connected graph that has one less edge than it has nodes. In a tree, when an edge (a, b) is deleted, the result is a forest of two disjointed trees. One tree contains node (a) and the other contains node (b). There are other properties, but this list gives us enough information for writing constraints in SQL. Remember, this is a book about programming, not graph theory. Therefore you will get just enough to help you write code, but not enough to be a mathematician.
Properties of Hierarchies
A hierarchy is a directed tree with extra properties: subordination and inheritance.
A hierarchy is a common way to organize a great many things, but the examples in this book will be organizational charts and parts explosions. These are two common business applications and can be easily understood by anyone without any special subject area knowledge. In addition, they demonstrate that the relationship represented by the edges of the graph can run from the root or up to the root.
In an organizational chart authority starts at the root, with the president of the enterprise, head of the army, or whatever the organization is, and it flows downward. Look at a military chain of command. If you are a private and your sergeant is killed, you still have to take orders from your captain.
Subordination is inherited from the root downward. In a parts explosion the relationship we are modeling runs “up the tree” to the root, or final assembly. If you are missing any subassembly, you cannot get a final assembly.
Inheritance, either to or from the root, is the most important property of a hierarchy. This property does not exist in an ordinary tree. If I delete an edge in a tree, I now have two separate trees.
Another property of a hierarchy is that the same node can play many different roles. In an organizational chart one person might hold several different jobs; in a parts explosion the same kind of screw, nut, or washer will appear in many different subassemblies. Moreover, the same subassembly can appear in many places. To make this more concrete, imagine a restaurant with a menu. The menu disassembles into dishes, and each dish disassembles into ingredients, and each ingredient is either simple (e.g., salt, pepper, flour), or it is a recipe, itself, such as béarnaise sauce or hollandaise sauce. These recipes might include further recipes. For example, béarnaise sauce is essentially hollandaise, with vinegar substituted for the water, and the addition of shallots, tarragon, chervil, and (sometimes) parsley, thyme, bay leaf, and cayenne pepper.
Hierarchies have roles that are filled by entities. This role property does not exist in a tree; each node appears once in a tree and is unique.
Types of Hierarchies
Getting away from looking at the world from the viewpoint of a casual mathematician, let’s look at it from the viewpoint of a casual database systems designer. What kinds of data situations will I want to model? Looking at the world from a very high level, I can see following four kinds of modeling problems:
- Static nodes and static edges. For example, a chart of accounts in an accounting system will probably not change much over time. This is probably best done with a hierarchical encoding scheme rather than a table. We will talk about such encoding schemes later in this book.
- Static nodes and dynamic edges, For example, an Internet Newsgroup message board. Obviously you cannot add a node to a tree without adding an edge, but the content of the messages (nodes) never change once they are posted; however, new replies can be posted as subordinates to any existing message (edge).
- Dynamic nodes and static edges. This is the classic organizational chart in which the organization stays the same, but the people holding the offices rotate frequently. This is assuming that your company does not reorganize more often than its personnel turns over.
- Dynamic nodes and dynamic edges. Imagine that you have a graph model of a communications or transportation network. The traffic on the network is constantly changing. You want to find a minimal spanning tree based on the current traffic and update that tree as the nodes and edges come on and off the network. To make this a little less abstract, the fastest path from the fire station to a particular home address will not necessarily be the same route at 05:00 Hrs as it will be at 17:00 Hrs. Once the fire is put out, the node that represented the burning house can disappear from the tree and the next fire location becomes a to which we must find a path.
Looking at the world from another viewpoint, we might classify hierarchies by usage—as either searching or reporting. An example of a searching hierarchy is the Dewey Decimal system in a library. You move from the general classifications to a particular book—down the hierarchy. An example of a reporting hierarchy is an accounting system. You move from particular transactions to summaries by general categories (e.g., assets, liabilities, equity)—up the hierarchy.
You might pick a different tree model for a table in each of these situations to get better performance. It can be a very hard call to make, and it is hard to give even general advice. Hopefully, I can show you the tradeoffs and you can make an informed decision.
Note on Recursion
I am going to take a little time to explain recursion, because trees are a recursive data structure and can be accessed by recursive algorithms. Many commercial programmers who are old enough to spell “Cobol” in uppercase letters are not familiar with the concept of recursion. Recursion does not appear in early programming languages. Even when it did, or was added later, as was the case in IBM’s MVS Cobol product in 1999, most programmers do not use it.
There is an old geek joke that gives the dictionary definition: Recursion = (REE - kur - shun) self-referencing; also see recursion. This is pretty accurate, if not all that funny. A recursive structure is composed of smaller structures of the same kind. Thus a tree is composed of subtrees. You finally arrive at the smallest possible subtrees, the leaf nodes—a subtree of size one.
A recursive function is also like that; part of its work is done by invoking itself until it arrives at the smallest unit of work for which it can return an answer. Once it gets the lowest level answer, it passes it back to the copy of the function that called it, so that copy can finish its computations, and so forth until we have gotten back up the chain to the first invocation that started it all.
It is very important to have a halting condition in a recursive function for obvious reasons.
Perhaps the idea will be easier to see with a simple example. Let’s reverse a string with the following function:
CREATE FUNCTION Reverse (IN instring VARCHAR(20))
RETURNS VARCHAR(20)
LANGUAGE SQL
DETERMINISTIC
BEGIN –– recursive function
IF CHAR_LENGTH(instring) IN (0, 1) –– halt condition
THEN RETURN (instring);
ELSE RETURN –– flip the two halves around, recursively
(Reverse(SUBSTRING (instring FROM (CHAR_LENGTH(instring)/2 + 1))
|| Reverse(SUBSTRING (instring FROM 1 FOR
CHAR_LENGTH(instring)/2))));
END IF;
END;
This becomes:
(Reverse(Reverse(‘e’) || Reverse(‘d’))
|| Reverse(Reverse(‘c’) || Reverse(‘ab’))
This becomes:
((‘e’||’d’)
|| ((‘c’) || Reverse((Reverse(‘b’) || Reverse(‘a’))))
This finally becomes:
((‘e’||‘d’) || (‘c’ || (‘b’||‘a’)))
In the case of trees we will test to see if a node is either the root or a leaf node as our halting conditions. The rest of the time we are dealing with a subtree, which is just another tree. This is why a tree is called a “recursive structure.”
--
Joe Celko was a member of the ANSI X3H2 Database Standards Committee and helped write the SQL-92 standards. He is the author of over 750 magazine columns and seven books, the best known of which is SQL for Smarties, now in its third edition. For more articles, puzzles, resources, and more, go to www.celko.com.
Contributors : Joe Celko
Last modified 2005-09-08 08:47 AM
